Mẫu nguyên tử Bolà sự phối hợp giữa mẫu nguyên tử Rutherford cùng với 2 tiên đề Bo về các trạng thái dừng, các quỹ đạo dừng và về sự hấp thụ và bức xạ năng lượng của nguyên tử. Thông qua những nội dung được đề cập tới trong bài học, mời các bạn cùng nghiên cứu bài 33- Mẫu nguyên tử Bo.
Năm 1911, Rutherford mạnh dạn đề sướng mẫu hành tinh nguyên tử: Theo Rutherford nguyên tử được cấu tạo bởi hạt nhân mang tích điện dương nằm ở chính giữa, xung quanh có các electron mang điện tích âm chuyển động trên các quỹ đạo tròn hay elíp giống như hệ Mặt Trời nên gọi là mẫu hành tinh nguyên tử.
Mẫu hành tinh nguyên tử của Rơ-dơ-pho gặp phải khó khăn là không giải thích được tính bền vững của các nguyên tử và sự tao thành quang phổ vạch của các nguyên tử.
Mẫu nguyên tử của Bo bao gồm mô hình hành tinh nguyên tử và hai tiên đề của Bo.
Nguyên tử chỉ tồn tại trong một số trạng thái có năng lượng xác định En, gọi là các trạng thái dừng. Khi ở trạng thái dừng, nguyên tử không bức xạ.
Trong các trạng thái dừng của nguyên tử, electron chuyển động quanh hạt nhân trên những quỹ đạo có bán kính hoàn toàn xác định gọi là quỹ đạo dừng.
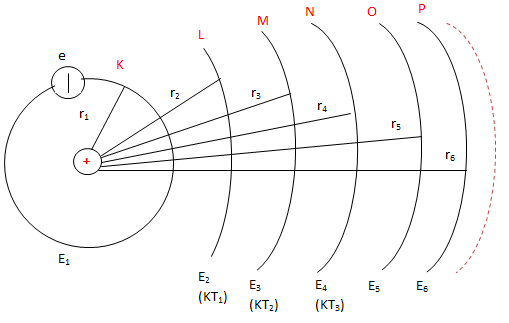
Bán kính quỹ đạo dừng của electron trong nguyên tử hyđrô:
\(r_n=n^2.r_0\), với n là số nguyên và \(r_0=5,3.10^{-11}(m)\), là bán kính Bo.
Bình thường, nguyên tử ở trạng thái dừng có năng lượng thấp nhất gọi là trạng thái cơ bản. Khi hấp thụ năng lượng thì nguyên tử chuyển lên trạng thái dừng có năng lượng cao hơn, gọi là trạng thái kích thích. Thời gian nguyên tử ở trạng thái kích thích rất ngắn (chỉ cỡ 10-8s). Sau đó nguyên tử chuyển về trạng thái dừng có năng lượng thấp hơn và cuối cùng về trạng thái cơ bản.
Khi nguyên tử chuyển từ trạng thái dừng có năng lượng \(E_n\) sang trạng thái dừng có năng lượng \(E_m\) nhỏ hơn thì nó phát ra một phôtôn có năng lượng:
\(\varepsilon _{nm}=h.f{nm}=E_n-E_m\).

Ngược lại, nếu nguyên tử đang ở trạng thái dừng có năng lượng \(E_m\) mà hấp thụ được một phôtôn có năng lượng \(h.f\) đúng bằng hiệu \(E_n-E_m\) thì nó chuyển sang trạng thái dừng có năng lượng \(E_n\) lớn hơn.
Mẫu nguyên tử Bo giải thích được các quy luật của quang phổ nguyên tử Hyđrô.
Khi electron chuyển từ mức năng lương cao (\(E_{cao}\)) xuống mức năng lượng thấp hơn (\(E_\) thấp) thì nó phát ra một phôtôn có năng lượng hoàn toàn xác định: \(h.f\) = \(E_{cao}\) – \(E_\) thấp.
Mỗi phôtôn có tần số f ứng với một sóng ánh sáng đơn sắc có bước sóng \(\lambda =\frac{c}{f}\) , tức là ứng với một vạch quang phổ có một màu nhất định.
Ngược lại, nếu một nguyên tử hyđrô đang ở một mức năng lương \(E_\) thấp nào đó mà nằm trong một chùm ánh sáng trắng, trong đó có tất cả các phôtôn có năng lượng từ lớn đến nhỏ khác nhau, thì lập tức nguyên tử đó sẽ hấp thụ ngay một phôtôn có năng lượng phù hợp \(\varepsilon =h.f\) = \(E_{cao}\) – \(E_\) thấp để chuyển lên mức năng lượng \(E_{cao}\). Như vậy một sóng ánh sáng đơn sắc đã bị hấp thụ làm cho trên nền quang phổ liên tục xuất hiện một vạch tối.
Khi nguyên tử hidro ở trạng thái n thì năng lượng và bán kính được xác định \(E_n=-\frac{13,6}{n^2}\) và \(r_n=n^2.r_0\), với \(n_0=5,3.10^{-11}(m)\). Khi bán kính của electron bằng 2,12.10-10 (m) thì năng lượng của nó bằng bao nhiêu?
Ta có
\(r_n=n^2.r_0\)
\(\Rightarrow 2,12.10^{-10}=n^2.5,3.10^{-11}\Rightarrow n^2=4\)
⇒ Năng lượng \(E_n=\frac{13,6}{n^2}=-\frac{13,6}{4}=-3,4 \ eV\)
Khi nguyên tử hidro chuyển từ trạng thái E4 về E2 thì phát ra photon có bước sóng \(\lambda _{42}\). Khi nguyên tử hidro chuyển từ trạng thái E5 về E3 thì phát ra photon có bước sóng \(\lambda _{53}\). Tìm \(\frac{\lambda _{53}}{\lambda _{42}}\) = ?
Ta có
\(\left.\begin{matrix} \varepsilon _{42}=\frac{hc}{\lambda _{42}}=E_4-E_2\\ \varepsilon _{53}=\frac{hc}{\lambda _{53}}=E_5-E_3 \end{matrix}\right\} \ \Rightarrow \frac{\varepsilon _{42}}{\varepsilon _{53}}=\frac{\lambda _{53}} {\lambda _{42}}=\frac{E_4-E_2}{E_5-E_3}\)
\(\Rightarrow \frac{\lambda _{53}}{\lambda _{42}}=\frac{-\frac{13,6}{4^2} -(-\frac{13,6}{2^2})}{-\frac{13,6}{5^2}-(-\frac{13,6}{3^2})}\)
\(\Rightarrow \frac{\lambda _{53}}{\lambda _{42}}=\frac{-\frac{1}{4^2}+\frac{1}{2^2}} {-\frac{1}{5^2}+\frac{1}{3^2}}=\frac{675}{256}\)
\(\Rightarrow \frac{\lambda _{53}}{\lambda _{42}}=\frac{675}{256}\)
Qua bài giảng Mẫu nguyên tử Bo này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
Trình bày được mẫu nguyên tử Bo.
Phát biểu được hai tiên đề của Bo về cấu tạo nguyên tử.
Giải thích được tại sao quang phổ phát xạ và hấp thụ của nguyên tử hiđrô lại là quang phổ vạch.
Vận dụng công thức cơ bản vào giải quyết một số bài tập dạng trắc nghiệm
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Vật lý 12 Bài 33 cực hay có đáp án và lời giải chi tiết.
Trong quang phổ của nguyên tử hiđro, ba vạch đầu tiên trong dãy Lai man có bước sóng \(\lambda _{12}=121,6 nm\) ; \(\lambda _{13}=102,6 nm\) ; \(\lambda _{14}=97,3 nm\). Bước sóng của vạch đầu tiên trong dãy Banme và vạch đầu tiên trong dãy Pasen là
Electron đang ở quỹ đạo n chưa rõ thì chuyển về quỹ đạo L và thấy rẳng bán kính quỹ đạo đã giảm đi 4 lần. Hỏi ban đầu electron đang ở quỹ đạo nào?
Khi nguyên tử hidro ở trạng thái n thì năng lượng và bán kính được xác định \(E_n=-\frac{13,6}{n^2}\) và \(r_n=n^2.r_0\), với \(n_0=5,3.10^{-11}(m)\). Khi bán kính của electron bằng 2,12.10-10 (m) thì năng lượng của nó bằng bao nhiêu?
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
Các em có thể xem thêm phần hướng dẫn Giải bài tập Vật lý 12 Bài 33để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Bài tập 1 trang 169 SGK Vật lý 12
Bài tập 2 trang 169 SGK Vật lý 12
Bài tập 3 trang 169 SGK Vật lý 12
Bài tập 4 trang 169 SGK Vật lý 12
Bài tập 5 trang 169 SGK Vật lý 12
Bài tập 6 trang 169 SGK Vật lý 12
Bài tập 7 trang 169 SGK Vật lý 12
Bài tập 33.1 trang 94 SBT Vật lý 12
Bài tập 33.2 trang 94 SBT Vật lý 12
Bài tập 33.3 trang 94 SBT Vật lý 12
Bài tập 33.4 trang 94 SBT Vật lý 12
Bài tập 33.5 trang 95 SBT Vật lý 12
Bài tập 33.6 trang 95 SBT Vật lý 12
Bài tập 33.7 trang 95 SBT Vật lý 12
Bài tập 33.8 trang 95 SBT Vật lý 12
Bài tập 33.9 trang 96 SBT Vật lý 12
Bài tập 33.10 trang 96 SBT Vật lý 12
Bài tập 33.11 trang 96 SBT Vật lý 12
Bài tập 33.12 trang 96 SBT Vật lý 12
Bài tập 33.13 trang 97 SBT Vật lý 12
Bài tập 33.14 trang 97 SBT Vật lý 12
Bài tập 33.15 trang 97 SBT Vật lý 12
Bài tập 33.16 trang 97 SBT Vật lý 12
Bài tập 33.17 trang 97 SBT Vật lý 12
Bài tập 33.18 trang 97 SBT Vật lý 12
Bài tập 33.19 trang 98 SBT Vật lý 12
Bài tập 33.20 trang 98 SBT Vật lý 12
Bài tập 1 trang 241 SGK Vật lý 12 nâng cao
Bài tập 2 trang 241 SGK Vật lý 12 nâng cao
Bài tập 3 trang 241 SGK Vật lý 12 nâng cao
Bài tập 4 trang 241 SGK Vật lý 12 nâng cao
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Vật lý DapAnHay sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Vật Lý 12 DapAnHay
Trong quang phổ của nguyên tử hiđro, ba vạch đầu tiên trong dãy Lai man có bước sóng \(\lambda _{12}=121,6 nm\) ; \(\lambda _{13}=102,6 nm\) ; \(\lambda _{14}=97,3 nm\). Bước sóng của vạch đầu tiên trong dãy Banme và vạch đầu tiên trong dãy Pasen là
Electron đang ở quỹ đạo n chưa rõ thì chuyển về quỹ đạo L và thấy rẳng bán kính quỹ đạo đã giảm đi 4 lần. Hỏi ban đầu electron đang ở quỹ đạo nào?
Khi nguyên tử hidro ở trạng thái n thì năng lượng và bán kính được xác định \(E_n=-\frac{13,6}{n^2}\) và \(r_n=n^2.r_0\), với \(n_0=5,3.10^{-11}(m)\). Khi bán kính của electron bằng 2,12.10-10 (m) thì năng lượng của nó bằng bao nhiêu?
Khi nguyên tử hidro chuyển từ trạng thái E4 về E2 thì phát ra photon có bước sóng \(\lambda _{42}\). Khi nguyên tử hidro chuyển từ trạng thái E5 về E3 thì phát ra photon có bước sóng \(\lambda _{53}\). Xác định tỉ số \(\frac{\lambda _{53}}{\lambda _{42}}\) = ?
Mẫu nguyên tử Bo khác mẫu nguyên tử Rơ-dơ-pho ở điểm nào?
Nguyên tử hiđrô ở trạng tháy cơ bản được kích thích và chuyển lên trạng thái có bán kính quỹ đạo tăng lên 16 lần. Số bức xạ mà nguyên tử có thể phát ra là
Ở nguyên tử hidro, quỹ đạo nào sau đây có bán kính lớn nhất so với bán kính các quỹ đạo còn lại?
Đối với nguyên tử hiđrô, bán kính Bo là ro=5,3.10-11 m. Nguyên tử hiđrô có thể có bán kính nào sau đây?
Electron đang ở quỹ đạo n chưa rõ thì chuyển về quỹ đạo L và thấy rẳng bán kính quỹ đạo đã giảm đi 4 lần. Hỏi ban đầu electron đang ở quỹ đạo nào?
Năng lượng của êlectron trong nguyên tử hiđrô được tính theo công thức: En = -13,6 / n2; n = 1, 2, 3, … Xác định năng lượng ở quỹ đạo dừng L.
Trong nguyên tử hiđrô, bán kính Bo là r0 = 5,3.10-11 m. ở một trạng thái kích thích của nguyên tử hiđrô, êlectron chuyển động trên quỹ đạo dừng có bán kính là r = 2,12.10-10 m. Quỹ đạo đó có tên gọi là quỹ đạo dừng
A. L B. N.
C. O. D.M.
Để ion hoá nguyên tử hiđrô, người ta cần một năng lượng là 13,6 eV. Tính bước sóng ngắn nhất của vạch quang phổ có thể có được trong quang phổ của hiđrô.
Biết độ lớn của năng lượng toàn phần của êlectron trong nguyên tử hiđró thì tỉ lệ nghịch với độ lớn của bán kính quỹ đạo. Năng lượng toàn phần của êlectron gồm động năng của êlectron và thế năng tương tác của nó với hại nhân. Mặt khác, lại biết năng lượng toàn phần của êlectron trên quỹ đạo càng xa hạt nhân thì càng lớn. Gọi WK và WN là năng lượng toàn phần của êlectron trên các quỹ đạo K và N. Tính WN theo WK
Đối với nguyên tử hiđrô, khi êlectron chuyển từ quỹ đạo M về quỹ đạo K thì nguyên tử phát ra phôtôn có bước sóng 0,1026 μm. Tính năng lượng của phôtôn này theo eV.
Lấy h = 6,625.10-34 J.s ; e = 1,6.10-19 c và c = 3.108 m/s.
Khi êlectron ở quỹ đạo dừng thứ n thì năng lượng của nguyên tử hiđrô được xác định bởi công thức \({E_n} = \frac{{ - 13,6}}{{{n^2}}}\) (eV) (với n = 1, 2, 3,...). n = 1 ứng với trạng thái cơ bản và quỹ đạo K, gần hạt nhân nhất : n = 2, 3, 4... ứng với các trạng thái kích thích và các quỹ đạo L, M, N,...
a) Tính năng lượng của phôtôn (ra eV) mà nguyên tử hiđrô phải hấp thụ để êlectron của nó chuyển từ quỹ đạo K lên quỹ đạo N.
b) Ánh sáng ứng với phôtôn nói trên thuộc vùng quang phổ nào (hồng ngoại, tử ngoại, ánh sáng nhìn thấy...) ?
Cho h = 6,625.10-34J.S ; c = 3.108 m/s ; e = 1,6.10-19C.
Năng lượng của nguyên tử hiđrô ở các trạng thái dừng được xác định bởi công thức En = -13,6/n2(eV) (với n = 1, 2, 3,...). n = 1 ứng với trạng thái cơ bản (trạng thái K) ; n = 2, 3, 4... ứng với các trạng thái kích thích (các trạng thái L, M, N,...). Quang phổ của nguyên tử hiđrô trong vùng ánh sáng nhìn thấy có 4 vạch là : đỏ, lam, chàm và tím. Các vạch này ứng với sự chuyển của các nguyên tử hiđrô từ các trạng thái kích thích M, N, O, P vể trạng thái L Hãy tính bước sóng ánh sáng ứng với các vạch đỏ, lam, chàm và tím.
Cho h = 6,625.10-34 J.s ; c = 3.108 m/s ; e = 1,6.10-19 C.
Hiệu điện thế giữa anôt và catôt của một ống Rơn-ghen là U = 25 kV. Coi vận tốc ban đầu của chùm êỉectron phát ra từ catôt bằng không. Biết hằng số Plăng h = 6,625.10-34 ; điện tích nguyên tố bằng 1,6.10-19 C. Tính tần số lớn nhất của tia Rơn-ghen mà ống này có thể phát ra.
Trạng thái dừng của một nguyên tử là
A. Trạng thái đứng yên của nguyên tử.
B. Trạng thái chuyển động đều của nguyên tử.
C. Trạng thái trong đó mọi electron của nguyên tử đều không chuyển động đối với hạt nhân.
D. Một trong số các trạng thái có năng lượng xác định, mà nguyên tử có thể tồn tại.
Ở trạng thái dừng, nguyên tử
A. Không bức xạ và không hấp thụ năng lượng.
B. Không bức xạ, nhưng có thể hấp thụ năng lượng.
C. Không hấp thụ, nhưng có thể bức xạ năng lượng.
D. Vẫn có thể hập thụ và bức xạ năng lượng.
Dãy Ban – me ứng với sự chuyển electron từ quỹ đạo ở xa hạt nhân về quỹ đạo nào sau đây?
A. Quỹ đạo K.
B. Quỹ đạo L.
C. Quỹ đạo M.
D. Quỹ đạo N.
Bước sóng của vạch quang phổ thứ nhất trong dãy Lai- man là \({\lambda _0} = 122\) nm của hai vạch \({H_\alpha },{H_\beta }\) lần lượt là \({\lambda _1} = 0,656\mu m\) và \({\lambda _2} = 0,486\mu m\). Hãy tính bước sóng hai vạch tiếp theo trong dãy Lai- man và vạch đầu tiên trong dãy Pa-sen.
Họ và tên
Tiêu đề câu hỏi
Nội dung câu hỏi
Câu trả lời của bạn
Dãy Pasen:
\(\lambda _{max}=\lambda _{43}=\frac{hc}{E_{43}}=\frac{hc}{E_4-E_3}\)
\(\Rightarrow \lambda _{43}=\frac{6,625.10^{-34}.3.10^{8}}{\left ( -\frac{13,6}{4^2}+ \frac{13,6}{^2} \right ).1,6.10^{-19}}=1,878.10^{-19}m\)
Câu trả lời của bạn
\(\lambda _{21}=\lambda _{L1}; \lambda _{31}=\lambda _{L2};\lambda _{\alpha }=\lambda _{32}\)
\(E_{32}=E_3-E_2=E_3-E_1-(E_2-E_1)=E_{31}-E_21\)
\(\Rightarrow \frac{1}{\lambda _3_2}=\frac{1}{\lambda _3_1}-\frac{1}{\lambda _2_1} \Rightarrow \lambda _3_2=\frac{\lambda _2_1.\lambda _3_1}{\lambda _2_1-\lambda _3_1}\)
\(\Rightarrow \lambda _{32}=\frac{\lambda _L_1.\lambda _L_2}{\lambda _L_1-\lambda _L_2}\)
Câu trả lời của bạn
\(\lambda _{21}=0,1220\mu m;\lambda _{32}=0,6530\mu m\)
Vạch thứ 2 của dãy Laiman: \(\lambda _{31}\)
\(\frac{1}{\lambda _3_1}=\frac{1}{\lambda _3_2}+\frac{1}{\lambda _2_1} \Rightarrow \lambda _{31}=0,1028\mu m\)
Câu trả lời của bạn
Qũy đạo N ⇔ Mức NL E4
+ Số vạch tối đa: \(\frac{4*3}{2}=6\) vạch
Câu trả lời của bạn
Qũy đạo M ⇔ Mức NL E3
Câu trả lời của bạn
Qũy đạo O ⇔ Mức NL E5
+ Lai man: 5 – 1 = 4
+ Ban me: 5 – 2 = 3
+ Pa sen: 5 – 3 = 2
Câu trả lời của bạn
rn = 25r0 ⇒ n = 5
Bước sóng nhỏ nhất: \(\lambda _{51} = \frac{hc}{13,6.1,6.10^{-19}}\left ( 1-\frac{1}{25} \right ) = 0,095\ \mu m\)
Câu trả lời của bạn
K – L – M – N
⇒ rN = 42.rK = 84,8.10-11 (m)
Câu trả lời của bạn
Khi e chuyển từ quỹ đạo L về quỹ đạo K thì phát phát ra photon có năng lượng:
\(\Delta E = -\frac{1}{2^2} – \left ( -\frac{1}{1^2} \right ) = \frac{3E_0}{4}\ (eV)\)
Ta có:
\(\Delta E \sim \frac{1}{\lambda }\)
\(\\ \Rightarrow \Delta E_1 . \lambda _1 = \Delta E_2 . \lambda _2 \\ \Rightarrow \lambda _2 = \frac{\Delta E_1 . \lambda _1}{\Delta E_2} = \frac{\frac{5E_0}{36}.\lambda _0}{\frac{3E_0}{4}} = \frac{5\lambda _0}{27}\)
Câu trả lời của bạn
Tỉ số \(\frac{V_{L}}{V_{N}}\) bằng 2.
Câu trả lời của bạn
Ta có \(I=\frac{\left | \Delta q \right |}{\Delta t}\)
Nguyên tử hidro hạt nhân gồm có 1 proton và 1 electron chuyển động tròn xung quanh proton. Xét trong một chu kì (thời gian để electron chuyển động hết 1 vòng xung quanh proton) thì lượng \(\Delta q\)dịch chuyển là 1e \(\Rightarrow I=\frac{\left | e \right |}{T}\)
Ta có
Fđ = Fht \(\Rightarrow \frac{ke^2}{r^2}=m(\frac{2\pi}{T})^2r\Rightarrow \frac{1}{T^2} \sim \frac{1}{r^3}=\frac{1}{(n^2r_0)^3}\Rightarrow \frac{1}{T^2} \sim \frac{1}{n^6}\)
\(\Rightarrow \frac{1}{T^2} \sim \frac{1}{n^3}\Rightarrow I\sim \frac{1}{n^3}\)
Ta có \(I_2/I_1=n_1^3/n_2^3=2^3/4^3=1/8\)
Câu trả lời của bạn
Ở đây lực tĩnh điện đóng vai trò là lực hướng tâm
Fđ = Fht
\(\Rightarrow \frac{kq^2}{r^2}=\frac{mv^2}{r}\)
\(\Rightarrow v=\sqrt{\frac{kq^2}{rm}}(k=9.10^9)\)
\(=2,19.10^6(m/s)\)
Câu trả lời của bạn
rn = n2 r0 với n = 1, 2, 3,… ⇒ rn phải là một số nguyên lần chính phương của r0
Câu trả lời của bạn
\(\left\{\begin{matrix} \omega =\frac{v}{r_n}\\ v=\sqrt{\frac{k.e^2}{m.r_n}}\\ r_0=r_0.n^2 \end{matrix}\right.\)
\(\begin{matrix} n_k=1\\ n_M=3 \end{matrix}\)
\(\rightarrow \omega _M=\frac{\omega }{27}\)
Câu trả lời của bạn
\(\Delta E=E_n-E_m=-\frac{13,6}{m^2}+\frac{13,6}{n^2}\)
Với \(\left\{\begin{matrix} n=1\\ m=4 \end{matrix}\right.\rightarrow \Delta E=12,75eV\)
Với \(\left\{\begin{matrix} n=1\\ m=2 \end{matrix}\right.\rightarrow \Delta E=10,2eV\)
Câu trả lời của bạn
L ứng với n = 2, N ứng với n = 4 do đó bán kính giảm là
\((4^2-2^2)r_0=12r_0\)
Câu trả lời của bạn
12,75 eV
Câu trả lời của bạn
Ta có: r = r0 n2 ; Quỹ đạo K ứng n =1; Quỹ đạo L ứng n =2; M ứng n =3 ; N ứng n =4
Vậy: \(\frac{r_{N}}{r_{L}}=\frac{r_{0}.4^2}{r_{0}.2^2}=4\)
Câu trả lời của bạn
Bước sóng dài nhất phát ra khi chuyển trạng thái dừng từ E3 xuống E2. Bước sóng ngắn nhất phát ra khi chuyển từ E3 xuống E1.
Có \(\frac{\lambda _{max}}{\lambda _{min}} = \frac{E_3 – E_1}{E_3 – E_2}= \frac{32}{5}\)
Câu trả lời của bạn
Áp dụng công thức ta có
\(\varepsilon = – \frac{13,6 eV}{5^2} – ( – \frac{13,6 eV}{2^2}) = \frac{357}{125}eV\)

0 Bình luận
Để lại bình luận
Địa chỉ email của hạn sẽ không được công bố. Các trường bắt buộc được đánh dấu *