Chúng ta vừa kết thúc chương đầu tiên của phân môn Đại số 9, đây là kiến thức nền tảng giúp các em biết và vận dụng để giải các bài toán. Đây là bài ôn tập toàn bộ chương I, giúp các em nắm chắc kiến thức bằng lý thuyết và các bài tập minh họa.
1. \(\sqrt{A^2}=|A|\)
2. \(\sqrt{AB}=\sqrt{A}.\sqrt{B}\) (với \(A\geq 0;B\geq 0\))
3. \(\sqrt{\frac{A}{B}}=\frac{\sqrt{A}}{\sqrt{B}}\) (với \(A\geq 0;B>0\))
4. \(\sqrt{A^2B}=|A|\sqrt{B}\) (với \(B\geq 0\))
5. \(A\sqrt{B}=\sqrt{A^2B}\) (với \(A\geq 0;B\geq 0\))
\(A\sqrt{B}=-\sqrt{A^2B}\) (với \(A<0;B\geq 0\))
6. \(\sqrt{\frac{A}{B}}=\frac{1}{|B|}\sqrt{AB}\) (với \(AB\geq 0;B\neq 0\))
7. \(\frac{A}{\sqrt{B}}=\frac{a\sqrt{B}}{B}\) (với \(B>0\))
8. \(\frac{C}{\sqrt{A}\pm B}=\frac{C(\sqrt{A}\mp B)}{A-B^2}\) (với \(A\geq 0;A\neq B^2\))
9. \(\frac{C}{\sqrt{A}\pm \sqrt{B}}=\frac{C(\sqrt{A}\mp \sqrt{B})}{A-B}\) (với \(A\geq 0;B\geq 0;A\neq B\))
Bài 1: Tính cạnh của một hình vuông, biết rằng diện tích hình vuông đó bằng diện tích hình chữ nhật có chiều dài là \(16m\) và chiều rộng là \(9m\).
Hướng dẫn: Diện tích của hình chữ nhật là: \(16.9=144(m^2)\)
Theo đề, diện tích hình vuông bằng diện tích hình chữ nhật nên cạnh a của hình vuông là: \(a^2=\sqrt{144}\Leftrightarrow a=12(m)\)
Bài 2: Giải phương trình: \(x^2-2\sqrt{13}x+13=0\)
Hướng dẫn:
\(x^2-2\sqrt{13}x+13=0\) \(\Leftrightarrow x^2-2\sqrt{13}x+(\sqrt{13})^2=0\)\(\Leftrightarrow (x-\sqrt{13})^2=0\)
\(\Leftrightarrow x=\sqrt{13}\)
Bài 3: Không dùng máy tính, so sánh hai số \(\sqrt{16+64}\) và \(\sqrt{16}+\sqrt{64}\). Từ đó rút ra nhận xét gì
Hướng dẫn: \(\sqrt{16+64}=\sqrt{80}=4\sqrt{5}\)
\(\sqrt{16}+\sqrt{64}=4+8=12\)
Vậy \(\sqrt{16}+\sqrt{64}>\sqrt{16+64}\)
Bài 4: Không dùng máy tính, so sánh hai số \(\sqrt{100-64}\) và \(\sqrt{100}-\sqrt{64}\). Từ đó rút ra nhận xét gì
Hướng dẫn: \(\sqrt{100-64}=\sqrt{36}=6\)
\(\sqrt{100}-\sqrt{64}=10-8=2\)
Vậy \(\sqrt{100-64}>\sqrt{100}-\sqrt{64}\)
Nhận xét: Với hai số dương a, b, \(a>b\) ta có: \((\sqrt{a}-\sqrt{b})^2=a+b-2\sqrt{ab}\)
\((\sqrt{a-b})^2=a-b\)
\((\sqrt{a-b})^2-(\sqrt{a}-\sqrt{b})^2=a-b-a-b+2\sqrt{ab}=2(\sqrt{ab}-b)\)
\(=2\sqrt{b}(\sqrt{a}-\sqrt{b})>0\)
Vậy \(\sqrt{a}-\sqrt{b}<\sqrt{a-b}\)
Bài 5: Rút gọn biểu thức chứa biến sau: \(\left ( 1+\frac{a+\sqrt{a}}{\sqrt{a}+1} \right )\left ( 1-\frac{a-\sqrt{a}}{\sqrt{a}-1} \right )\)
Hướng dẫn:
Điều kiện: \(a\geq 0;a\neq 1\)
Với điều kiện trên:
\(\left ( 1+\frac{a+\sqrt{a}}{\sqrt{a}+1} \right )\left ( 1-\frac{a-\sqrt{a}}{\sqrt{a}-1} \right )\)
\( = \left( {1 + \sqrt a } \right).\left( {1 - \sqrt a } \right)\)\(=1-a\)
Bài 6: Thực hiện phép tính: \(A=\sqrt{5+\sqrt{24}}+\sqrt{5-\sqrt{24}}\)
Hướng dẫn: Do A dương nên bình phương đẳng thức, ta được:
\(A^2=5+5+\sqrt{24}-\sqrt{24}+2\sqrt{(5+\sqrt{24})(5-\sqrt{24})}=12\)
Vậy \(A=3\sqrt{2}\)
Bài 7: Giải phương trình: \(\sqrt{2x-1}+\sqrt{x}=2\)
Hướng dẫn:
Điều kiện: \(x\geq \frac{1}{2}\)
Với điều kiện trên, đặt \(\sqrt{2x-1}=a(a\geq 0);\sqrt{x}=b(b\geq 0)\)
Ta có: \(a^2=2x-1;b^2=x\)\(\Rightarrow a^2-2b^2=-1\)
Mặc khác: \(a+b=2\)
Ta đưa vào hệ: \(\left\{\begin{matrix} a+b=2\\ a^2-2b^2=-1 \end{matrix}\right.\)
Giải hệ trên bằng phương pháp thế:
\(\left\{\begin{matrix} a=1\\ b=1 \end{matrix}\right.\) (nhận) và \(\left\{\begin{matrix} a=7\\ b=-5 \end{matrix}\right.\)(không nhận)
Với \(a=1\Leftrightarrow x=1\)
Vậy \(x=1\) là nghiệm duy nhất của phương trình
-- Mod Toán Học 9 DapAnHay
Thực hiện phép tính \(5\sqrt{12}+2\sqrt{75}-5\sqrt{48}+4\sqrt{147}\)
Rút gọn biểu thức \(\sqrt{\frac{4}{(2-\sqrt{5})^2}}-\sqrt{\frac{4}{(2+\sqrt{5})^2}}\) là:
Giá trị của biểu thức \(A=\sqrt{2+\sqrt{3}+\sqrt{4-2\sqrt{3}-\sqrt{(2\sqrt{3}-3)^2}}}\) là:
Cho \(B=\left ( 1-\frac{4}{\sqrt{x}+1}+\frac{1}{x-1} \right ):\frac{x-2\sqrt{x}}{x-1}\) với \(x>0;x\neq 1;x\neq 4\)
Giá trị của x để \(B=2\) là:
Cho biểu thức \(C=\left ( \frac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\frac{\sqrt{x}-2}{x-1} \right )\frac{\sqrt{x}+1}{\sqrt{x}}\)với \(x>0;x\neq 1\)
Số nghiệm x thỏa bài toán để C nguyên là:
Khẳng định nào đúng
Giải phương trình: \(\sqrt x=-2\)
Nêu điều kiện để x là căn bậc hai số học của số a không âm. Cho ví dụ.
Chứng minh \(\sqrt {a^2} = |a|\) với mọi số a.
Biểu thức A phải thỏa mãn điều kiện gì để \(\sqrt A \) xác định?
Phát biểu và chứng minh định lí về mối liên hệ giữa phép nhân và phép khai phương. Cho ví dụ.
Phát biểu và chứng minh định lí về mối liên hệ giữa phép chia và phép khai phương. Cho ví dụ.
Tìm giá trị các biểu thức sau bằng cách biến đổi, rút gọn thích hợp
\(\displaystyle a)\sqrt {{{25} \over {81}}.{{16} \over {49}}.{{196} \over 9}}\)
\(\displaystyle b)\sqrt {3{1 \over {16}}.2{{14} \over {25}}.2{{34} \over {81}}}\)
\(\displaystyle c){{\sqrt {640} .\sqrt {34,3} } \over {\sqrt {567} }}\)
\(d)\sqrt {21,6} .\sqrt {810.} \sqrt {{{11}^2} - {5^2}}\)
Rút gọn các biểu thức sau:
a) \(\left( {\sqrt 8 - 3.\sqrt 2 + \sqrt {10} } \right)\sqrt 2 - \sqrt 5 \)
b) \(0,2\sqrt {{{\left( { - 10} \right)}^2}.3} + 2\sqrt {{{\left( {\sqrt 3 - \sqrt 5 } \right)}^2}} \)
c) \(\left( {{1 \over 2}.\sqrt {{1 \over 2}} - {3 \over 2}.\sqrt 2 + {4 \over 5}.\sqrt {200} } \right):{1 \over 8}\)
d) \(2\sqrt {{{\left( {\sqrt 2 - 3} \right)}^2}} + \sqrt {2.{{\left( { - 3} \right)}^2}} - 5\sqrt {{{\left( { - 1} \right)}^4}} \)
Phân tích thành nhân tử (với các số x, y, a, b không âm và a ≥ b)
a) \(xy - y\sqrt x + \sqrt x - 1\)
b) \(\sqrt {ax} - \sqrt {by} + \sqrt {bx} - \sqrt {ay} \)
c) \(\sqrt {a + b} + \sqrt {{a^2} - {b^2}} \)
d) \(12 - \sqrt x - x\)
Rút gọn rồi tính giá trị của các biểu thức sau:
a) \(\sqrt { - 9{\rm{a}}} - \sqrt {9 + 12{\rm{a}} + 4{{\rm{a}}^2}}\) tại a = - 9
b) \(1 + {{3m} \over {m - 2}}\sqrt {{m^2} - 4m + 4}\) tại m = 1,5
c) \(\sqrt {1 - 10{\rm{a}} + 25{{\rm{a}}^2}} - 4{\rm{a}}\) tại a = √2
d) \(4{\rm{x}} - \sqrt {9{{\rm{x}}^2} - 6{\rm{x}} + 1} \) tại x = √3
Tìm x, biết:
a) \(\sqrt {{{\left( {2{\rm{x}} - 1} \right)}^2}} = 3\)
b) \({5 \over 3}\sqrt {15{\rm{x}}} - \sqrt {15{\rm{x}}} - 2 = {1 \over 3}\sqrt {15{\rm{x}}} \)
Chứng minh các đẳng thức sau:
a) \(\left( {{{2\sqrt 3 - \sqrt 6 } \over {\sqrt 8 - 2}} - {{\sqrt {216} } \over 3}} \right).{1 \over {\sqrt 6 }} = - 1,5\)
b) \(\left( {{{\sqrt {14} - \sqrt 7 } \over {1 - \sqrt 2 }} + {{\sqrt {15} - \sqrt 5 } \over {1 - \sqrt 3 }}} \right):{1 \over {\sqrt 7 - \sqrt 5 }} = - 2\)
c) \({{a\sqrt b + b\sqrt a } \over {\sqrt {ab} }}:{1 \over {\sqrt a - \sqrt b }} = a - b\) với a, b dương và a ≠ b
d) \(\left( {1 + {{a + \sqrt a } \over {\sqrt a + 1}}} \right)\left( {1 - {{a - \sqrt a } \over {\sqrt a - 1}}} \right) = 1 - a\) với a ≥ 0 và a ≠ 1
Cho biểu thức
\(Q = {a \over {\sqrt {{a^2} - {b^2}} }} - \left( {1 + {a \over {\sqrt {{a^2} - {b^2}} }}} \right):{b \over {a - \sqrt {{a^2} - {b^2}} }}\) với a > b > 0
a) Rút gọn Q
b) Xác định giá trị của Q khi a = 3b
Nếu \(x\) thỏa mãn điều kiện:
\(\sqrt {3 + \sqrt x } = 3\)
Thì \(x\) nhận giá trị là
(A) \(0\)
(B) \(6\)
(C) \(9\)
(D) \(36\)
Hãy chọn câu trả lời đúng.
Biểu thức
\(\sqrt {\dfrac{{3 - \sqrt 5 }}{{3 + \sqrt 5 }}} + \sqrt {\dfrac{{3 + \sqrt 5 }}{{3 - \sqrt 5 }}} \)
Có giá trị là
(A) \(3\)
(B) \(6\)
(C) \(\sqrt 5 \)
(D) \( - \sqrt 5 \)
Hãy chọn câu trả lời đúng.
Chứng minh các đẳng thức:
a) \(\sqrt {2 + \sqrt 3 } + \sqrt {2 - \sqrt 3 } = \sqrt 6 \)
b) \(\sqrt {{4 \over {{{\left( {2 - \sqrt 5 } \right)}^2}}}} - \sqrt {{4 \over {{{\left( {2 + \sqrt 5 } \right)}^2}}}} = 8.\)
Cho:
\(A = \dfrac{{\sqrt {4{x^2} - 4x + 1} }}{{4x - 2}}\)
Chứng minh: \(\left| A \right| = 0,5\) với \(x \ne 0,5.\)
Rút gọn các biểu thức:
a) \(\sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} + \sqrt {4 - 2\sqrt 3 } ;\)
b) \(\sqrt {15 - 6\sqrt 6 } + \sqrt {33 - 12\sqrt 6 } ;\)
c) \(\left( {15\sqrt {200} - 3\sqrt {450} + 2\sqrt {50} } \right):\sqrt {10} .\)
a) Chứng minh:
\(x - 4\sqrt {x - 4} = {\left( {\sqrt {x - 4} - 2} \right)^2};\)
b) Tìm điều kiện xác định và rút gọn biểu thức:
\(\sqrt {x + 4\sqrt {x - 4} } + \sqrt {x - 4\sqrt {x - 4} } .\)
Tìm điều kiện xác định của các biểu thức sau:
\(A = \sqrt x + \sqrt {x + 1} \);
\(B = \sqrt {x + 4} + \sqrt {x - 1} .\)
a) Chứng minh rằng \(A \ge 1\) và \(B \ge \sqrt 5 \);
b) Tìm x, biết:
\(\sqrt x = \sqrt {x + 1} = 1\);
\(\sqrt {x + 4} + \sqrt {x - 1} = 2\)
Chứng minh:
\(x - \sqrt x + 1 = {\left( {\sqrt x - {\dfrac{1}{2}}} \right)^2} + {\dfrac{3}{4}}\) với \(x > 0\)
Từ đó, cho biết biểu thức \(\dfrac{1}{{x - \sqrt x + 1}}\) có giá trị lớn nhất là bao nhiêu ?
Giá trị đó đạt được khi \(x\) bằng bao nhiêu?
Họ và tên
Tiêu đề câu hỏi
Nội dung câu hỏi
Câu trả lời của bạn
Điều kiện của x để biểu thức A có nghĩa :\(\left\{ \begin{array}{l}x + 2 \ge 0\\{x^3} + 1 \ne 0\\\sqrt {x + 2} \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\x \ne - 1\end{array} \right.\)
Câu trả lời của bạn
\(A = \frac{{{x^2} - 2x}}{{{x^3} + 1}} + \frac{1}{2}.(\frac{1}{{1 + \sqrt {x + 2} }} + \frac{1}{{1 - \sqrt {x + 2} }}) = \frac{{x({x^{}} - 2)}}{{(x + 1)({x^2} - x + 1)}} + \frac{1}{2}.\frac{2}{{1 - (x + 2)}}\)
\( = \frac{{x({x^{}} - 2)}}{{(x + 1)({x^2} - x + 1)}} - \frac{1}{{x + 1}} = \frac{{x({x^{}} - 2) - ({x^2} - x + 1)}}{{(x + 1)({x^2} - x + 1)}}\)
\( = \frac{{ - (x + 1)}}{{(x + 1)({x^2} - x + 1)}} = \frac{{ - 1}}{{{x^2} - x + 1}}\)
Tìm giá trị nhỏ nhất của A.
Ta có \(A = \frac{{ - 1}}{{{x^2} - x + 1}} = \frac{{ - 1}}{{{{(x - \frac{1}{2})}^2} + \frac{3}{4}}}\)
Ta có A nhỏ nhất khi \({(x - \frac{1}{2})^2} + \frac{3}{4}\) đạt giá trị nhỏ nhất
Vậy: Giá trị nhỏ nhất của là A là \(\frac{{ - 4}}{3}\) khi \(x - \frac{1}{2}\) = 0\( \Leftrightarrow \)\(x = \frac{1}{2}\)
Câu trả lời của bạn
ĐK: \({\rm{ a}} \ne \pm b\sqrt 5 \) (*)
\(\begin{array}{l}\frac{2}{{a + b\sqrt 5 }} - \frac{3}{{a - b\sqrt 5 }} = - 9 - 20\sqrt 5 \\ \Leftrightarrow 2(a - b\sqrt 5 ) - 3(a + b\sqrt 5 ) = - (9 + 20\sqrt 5 )(a + b\sqrt 5 )(a - b\sqrt 5 )\end{array}\)
\( \Leftrightarrow 9{a^2} - 45{b^2} - a = \sqrt 5 ( - 20{a^2} + 100{b^2} + 5b) (*)\)
Ta thấy (*) có dạng \(A = B\sqrt 5 \) trong đó A, B \( \in Q\), nếu \(B \ne 0\,thi\,\sqrt 5 = \frac{A}{B} \in I\) vô lí vậy B = 0 ⇒ A= 0.
Do đó (*)\( \Leftrightarrow \left\{ \begin{array}{l}9{a^2} - 45{b^2} - a = 0\\ - 20{a^2} + 100{b^2} + 5b = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}9{a^2} - 45{b^2} - a = 0\\ - 9{a^2} + 45{b^2} + \frac{9}{4}b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9{a^2} - 45{b^2} - a = 0\\a = \frac{9}{4}b\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{9}{4}b\\{b^2} - 4b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 9\\b = 4\end{array} \right.\,\,\,\,hoac\left\{ \begin{array}{l}a = 0\\b = 0\end{array} \right.\) (không t/m ĐK (*)).
Vậy a = 9; b = 4
Câu trả lời của bạn
Ta có \(\sqrt {{{2015}^2} - 1} - \sqrt {{{2014}^2} - 1} = \frac{{(\sqrt {{{2017}^2} - 1} - \sqrt {{{2016}^2} - 1} )(\sqrt {{{2017}^2} - 1} + \sqrt {{{2016}^2} - 1} )}}{{\sqrt {{{2017}^2} - 1} + \sqrt {{{2016}^2} - 1} }}\)
\( = \frac{{({{2015}^2} - 1) - ({{2014}^2} - 1)}}{{\sqrt {{{2017}^2} - 1} + \sqrt {{{2016}^2} - 1} }} = \frac{{{{2017}^2} - {{2016}^2}}}{{\sqrt {{{2017}^2} - 1} + \sqrt {{{2016}^2} - 1} }} = \frac{{(2017 - 2016)(2017 + 2016)}}{{\sqrt {{{2017}^2} - 1} + \sqrt {{{2016}^2} - 1} }}\)
\( = \frac{{2017 + 2016}}{{\sqrt {{{2017}^2} - 1} + \sqrt {{{2016}^2} - 1} }} > \frac{{2.2016}}{{\sqrt {{{2017}^2} - 1} + \sqrt {{{2016}^2} - 1} }}\)
Vậy \(\sqrt {{{2017}^2} - 1} - \sqrt {{{2016}^2} - 1} > \frac{{2.2016}}{{\sqrt {{{2017}^2} - 1} + \sqrt {{{2016}^2} - 1} }}\)
Câu trả lời của bạn
\(x = \frac{{(\sqrt x - 1).\sqrt[3]{{{{(\sqrt 3 + 1)}^3}}}}}{{\sqrt {{{(\sqrt {20 + 1} )}^2}} + 3}} = \frac{{(\sqrt {3 - 1} )(\sqrt {3 + 1} }}{{\sqrt {20} + 4}}\)
\( = \frac{2}{{2(\sqrt 5 + 2)}} = \sqrt 5 - 2.\)
\( \Rightarrow {x^2} + 4x - 1 = 0 \Rightarrow P = - 1\)
Câu trả lời của bạn
\(x = 9 - \sqrt {{{\left( {\frac{2}{{\sqrt 5 - 2}}} \right)}^2}} + \sqrt {{{\left( {\frac{2}{{\sqrt 5 + 2}}} \right)}^2}} \)
\( = 9 - \frac{2}{{\sqrt 5 - 2}} + \frac{2}{{\sqrt 5 + 2}} = 9 - \frac{{2\sqrt 5 + 4 - 2\sqrt 5 + 4}}{{{{\left( {\sqrt 5 } \right)}^2} - {2^2}}} = 9 - 8 = 1\)
\(f(x) = f(1) = 1\)
Câu trả lời của bạn
\(\frac{{{x^2}}}{{x + y}} + \frac{{{y^2}}}{{y + z}} + \frac{{{z^2}}}{{z + x}} \ge \frac{{x + y + z}}{2}\) .
Theo bất đẳng thức Cauchy :
\(\frac{{x + y}}{2} \ge \sqrt {xy} ;\frac{{y + z}}{2} \ge \sqrt {yz} ;\frac{{z + x}}{2} \ge \sqrt {zx} \) nên \(\frac{{x + y + z}}{2} \ge \frac{{\sqrt {xy} + \sqrt {yz} + \sqrt {zx} }}{2} = \frac{1}{2}\)
\(\min A = \frac{1}{2} \Leftrightarrow x = y = z = \frac{1}{3}.\)
Câu trả lời của bạn
ĐKXĐ: \(3{x^3} - 19{x^2} + 33x - 9 \ne 0\)
⇔ \(x \ne \frac{1}{3}\) và \(x \ne 3\)
Câu trả lời của bạn
\(\frac{{3{x^3} - 14{x^2} + 3x + 36}}{{3{x^3} - 19{x^2} + 33x - 9}}\) (1 điểm)
= \(\frac{{{{(x - 3)}^2}(3x + 4)}}{{(3x - 1){{(x - 3)}^2}}}\)
= \(\frac{{3x + 4}}{{3x - 1}}\)
A = 0 ⇔ 3x + 4 = 0
⇔ x = \(\frac{{ - 4}}{3}\) (thỏa mãn ĐKXĐ)
Vậy với x = \(\frac{{ - 4}}{3}\) thì A = 0.
A = \(\frac{{3x + 4}}{{3x - 1}}\)= \(\frac{{3x - 1 + 5}}{{3x - 1}}\)= 1 + \(\frac{5}{{3x - 1}}\) (1 điểm)
Vì \(x \in Z\) ⇔ \(A \in Z\) ⇔ \(\frac{5}{{3x - 1}} \in Z\)⇔ 3x – 1 \( \in \) Ư(5)
mà Ư(5) = {-5;-1;1;5}

Vậy tại \(x\in\{0;2 \}\) thì \(A \in Z\)
\(A = \left( {\frac{{2x - 1 + \sqrt x }}{{1 - x}} + \frac{{2x\sqrt x + x - \sqrt x }}{{1 + x\sqrt x }}} \right).\frac{{\left( {x - \sqrt x } \right)\left( {1 - \sqrt x } \right)}}{{2\sqrt x - 1}} - 1\)
Câu trả lời của bạn
Điều kiện: \(x \ge 0;x \ne \frac{1}{4};x \ne 1\)
Đặt \(\sqrt x = a;a \ge 0 \Rightarrow x = {a^2}\)
Ta có:
\(\begin{array}{l} A = \left( {\frac{{2{a^2} - 1 + a}}{{1 - {a^2}}} + \frac{{2{a^3} + {a^2} - a}}{{1 + {a^3}}}} \right).\frac{{\left( {{a^2} - a} \right)\left( {1 - a} \right)}}{{2a - 1}} - 1\\ A = \left[ {\frac{{\left( {a + 1} \right)\left( {2a - 1} \right)}}{{\left( {1 - a} \right)\left( {a + 1} \right)}} + \,\frac{{a\,\left( {a + 1} \right)\left( {2a - 1} \right)}}{{\left( {a + 1} \right)\left( {{a^2} - a + 1} \right)}}} \right].\frac{{a\,\left( {a - 1} \right)\left( {1 - a} \right)}}{{2a - 1}} - 1\\ A = \left[ {\frac{{\left( {2a - 1} \right)}}{{\left( {1 - a} \right)}} + \,\frac{{a\,\left( {2a - 1} \right)}}{{\left( {{a^2} - a + 1} \right)}}} \right].\frac{{a\,\left( {a - 1} \right)\left( {1 - a} \right)}}{{2a - 1}} - 1\\ A = \left[ {\frac{1}{{\left( {1 - a} \right)}} + \,\frac{{a\,}}{{\left( {{a^2} - a + 1} \right)}}} \right].(2a - 1).\frac{{a\,\left( {a - 1} \right)\left( {1 - a} \right)}}{{2a - 1}} - 1\\ \Rightarrow A = \frac{{ - 1}}{{{a^2} - a + 1}}\\ \Leftrightarrow A = \frac{{ - 1}}{{x - \sqrt x + 1}}\\ A = \frac{{ - 1}}{{x - \sqrt x + 1}}\, < \, - \frac{1}{7}\,\,\\ \Leftrightarrow \,\frac{1}{{x - \sqrt x + 1}} > \frac{1}{7}\,\,\\ \Leftrightarrow x - \sqrt x + 1\,\, < 7 \end{array}\)
\(\begin{array}{l} Do\,\,\,\,x - \sqrt x + 1 = \,{\left( {\sqrt x - \frac{1}{2}} \right)^2} + \frac{3}{4} > 0\\ {x^{}} - \sqrt x - 6 < 0\\ \Leftrightarrow \left( {\sqrt x - 3} \right)\left( {\sqrt x + 2} \right) < 0\\ \Leftrightarrow \sqrt x - 3 < 0\\ \Leftrightarrow 0 \le x < 9 \end{array}\)
Câu trả lời của bạn
Đặt
\(\begin{array}{l} x = \frac{{2 + \sqrt 3 }}{{\sqrt 2 + \sqrt {2 + \sqrt 3 } }};\\ y = \frac{{2 - \sqrt 3 }}{{\sqrt 2 - \sqrt {2 - \sqrt 3 } }}\\ \Rightarrow x + y = \sqrt 2 ;xy = \frac{1}{3}\\ B = {x^5} + {y^5}\\ = ({x^3} + {y^3})({x^2} + {y^2}) - {x^2}{y^2}(x + y)\\ = \frac{{11\sqrt 2 }}{9} \end{array}\)
Chứng minh
\(\frac{1}{{{a^2} + {b^2} + {c^2}}} + \frac{{2021}}{{ab + bc + ca}} \ge 674\)
Câu trả lời của bạn
đề bài thiếu giả thiết
Cho biểu thức A: (căn x/2 - 1/căn x)*(x - căn x/căn x+1-x+căn x/ căn x -1)
a, rút gọn A
b, tìm các giá trị x để A<-4
Câu trả lời của bạn
Cái này hả bạn đây có phải là đề bài k
Cho x, y, z khác 0 và x + y + z = 10. Tìm GTNN của \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z}\)?
Giúp mình với ạ, tìm gg k ra :(
Câu trả lời của bạn
 giúp mk vs aj ! Thank kiu
giúp mk vs aj ! Thank kiu
Câu trả lời của bạn
dễ
Có j đó sai
bình phương vế trái ta được 16( ab + a^2.b^2) tới đây mình cũng chịu
giải phương trình x^2+4x+(√x^2-1)=2(√2x+3)-5
Câu trả lời của bạn
dễ
chịu


?????
Thu gọn biết thức
G=[√(1+2√(27√2 +1)) - √(5-3√2)] : √(3√2 -4)
Mong mọi người giúp
Thanks
Câu trả lời của bạn
khó
khó thế, bạn hỏi nơi khác đi

Câu trả lời của bạn
Cho x, y, z>0 và xyz=1.Chứng minh \({x^3} + {y^3} + {z^3} \ge x + y + z\)
Mình cần gấp ạ!
Câu trả lời của bạn
troi
troi
x3 + y3 + z3 – xyz – xyz – xyz - x2y – y2x – x2z – z2x - y2z – z2y + x2y + y2x + x2z + z2x+ y2z+ z2y ... ta phân tích từ bài đã cho ra (x+y+z)(z2+x2+y2-xy-yz-zx)=0.
Cái nào khó quá, mà hình như bài này trên vietjack có nè
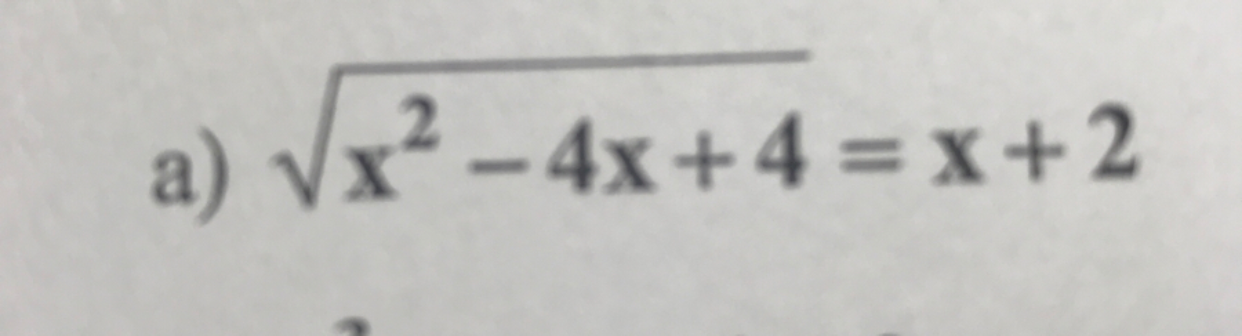
Câu trả lời của bạn

0 Bình luận
Để lại bình luận
Địa chỉ email của hạn sẽ không được công bố. Các trường bắt buộc được đánh dấu *