Đề bài
Câu 1:
Không sử dụng máy tính cầm tay, rút gọn biểu thức \(A = \sqrt {50} - \sqrt {32} + \sqrt 2 \).
Câu 2:
Không sử dụng máy tính cầm tay, giải hệ phương trình \(\left\{ \begin{array}{l}x + y = 4\\2x - y = 5\end{array} \right.\).
Câu 3:
Cho hàm số bậc nhất \(y = f\left( x \right) = \left( {\sqrt 3 - 1} \right)x + 1.\)
a) Hàm số trên là đồng biến hay nghịch biến trên \(\mathbb{R}?\) Vì sao?
b) Tính các giá trị: \(f\left( 0 \right);\,\,f\left( {\sqrt 3 + 1} \right).\)
Câu 4:
Tìm tọa độ giao điểm của hai đồ thị hàm số \(y = - 2{x^2}\) và \(y = x - 3.\)
Câu 5:
Cho biểu thức \(P = \left[ {\dfrac{{3x + 3\sqrt x - 3}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 1} \right)}} + \dfrac{1}{{\sqrt x + 2}} - \dfrac{{\sqrt x - 2}}{{\sqrt x - 1}}} \right]:\dfrac{{\sqrt x }}{{\sqrt x + 1}}\) với \(x > 0,\,\,x \ne 1\).
a) Rút gọn biểu thức \(P\).
b) Tìm giá trị của \(x\) để \(P > 0\).
Câu 6:
Ông Minh dự định đi bằng xe máy từ địa điểm A đến địa điểm B cách nhau 80 km trong thời gian định trước. Khi đi được 20 km, tại địa điểm C, xe của ông hỏng nên ông phải dừng lại để sửa xe mất 10 phút. Sau khi sửa xe xong, để đảm bảo thời gian như đã đinh, ông Minh tăng vận tốc thêm 5 km/h trên quãng đường đi từ C đến B. Hãy tính vận tốc xe của ông Minh trên quãng đường từ A đến C.
Câu 7:
Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(AB = 3cm,\,\,BC = 5cm.\) Tính độ dài cạnh \(AC\) và đường cao \(AH.\)
Câu 8:
Cho hai đường tròn \(\left( {{O_1};\,\,10\,cm} \right)\) và \(\left( {{O_2};\,\,15\,cm} \right)\) cắt nhau tại hai điểm phân biệt. Tiếp tuyến chung ngoài \(AB\) cắt đường thẳng \({O_1}{O_2}\) tại điểm \(C\) với \(A \in \left( {{O_1}} \right),\,\,B \in \left( {{O_2}} \right).\) Tính độ dài đoạn thẳng \({O_1}{O_2}\) biết \(C{O_1} = 40\,cm.\)
Câu 9:
Cho tam giác \(ABC\) cân tại \(A,\) các đường cao \(AM,\,\,BN\) cắt nhau tại \(H.\) Chứng minh \(MN\) là tiếp tuyến của đường tròn đường kính \(AH.\)
Câu 10:
Cho \(\Delta ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right),\) các đường cao \(AD,\,\,BE,\,\,CF\) cắt nhau tại \(H.\) Đường thẳng \(AD\) cắt đường tròn \(\left( O \right)\) tại \(M \ne A.\)
a) Chứng minh \(\Delta BHM\) cân.
b) Gọi \(P,\,\,Q\) lần lượt là điểm đối xứng với \(M\) qua \(AB\) và \(AC.\) Chứng minh ba điểm \(P,\,\,H,\,\,Q\) thẳng hàng.
Lời giải chi tiết
Câu 1.
Cách giải:
Không sử dụng máy tính cầm tay, rút gọn biểu thức \(A = \sqrt {50} - \sqrt {32} + \sqrt 2 \).
Ta có:
\(\begin{array}{l}A = \sqrt {50} - \sqrt {32} + \sqrt 2 \\A = \sqrt {{5^2}.2} - \sqrt {{4^2}.2} + \sqrt 2 \\A = 5\sqrt 2 - 4\sqrt 2 + \sqrt 2 \\A = 2\sqrt 2 \end{array}\)
Vậy \(A = 2\sqrt 2 \).
Câu 2.
Cách giải:
Không sử dụng máy tính cầm tay, giải hệ phương trình \(\left\{ \begin{array}{l}x + y = 4\\2x - y = 5\end{array} \right.\).
Ta có:
\(\left\{ \begin{array}{l}x + y = 4\\2x - y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 9\\y = 4 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 4 - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 1\end{array} \right.\).
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {3;1} \right)\).
Câu 3.
Cách giải:
Cho hàm số bậc nhất \(y = f\left( x \right) = \left( {\sqrt 3 - 1} \right)x + 1.\)
a) Hàm số trên là đồng biến hay nghịch biến trên \(\mathbb{R}?\) Vì sao?
Xét hàm số \(y = f\left( x \right) = \left( {\sqrt 3 - 1} \right)x + 1\) ta có: \(a = \sqrt 3 - 1 > 0\).
\( \Rightarrow \) Hàm số \(y = f\left( x \right) = \left( {\sqrt 3 - 1} \right)x + 1\) đồng biến trên \(\mathbb{R}.\)
b) Tính các giá trị: \(f\left( 0 \right);\,\,f\left( {\sqrt 3 + 1} \right).\)
Xét hàm số \(y = f\left( x \right) = \left( {\sqrt 3 - 1} \right)x + 1\) ta có: \(\left\{ \begin{array}{l}f\left( 0 \right) = \left( {\sqrt 3 - 1} \right).0 + 1 = 1\\f\left( {\sqrt 3 + 1} \right) = \left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right) + 1 = 3 - 1 + 1 = 3\end{array} \right..\)
Vậy \(f\left( 0 \right) = 1\) và \(f\left( {\sqrt 3 + 1} \right) = 3.\)
Câu 4.
Cách giải:
Tìm tọa độ giao điểm của hai đồ thị hàm số \(y = - 2{x^2}\) và \(y = x - 3.\)
Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là:
\( - 2{x^2} = x - 3 \Leftrightarrow 2{x^2} + x - 3 = 0\)
Phương trình có: \(a + b + c = 2 + 1 - 3 = 0\).
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt:\({x_1} = 1\) và \({x_2} = \dfrac{c}{a} = - \dfrac{3}{2}.\)
+) Với \(x = 1 \Rightarrow y = - {2.1^2} = - 2\).
+) Với \(x = - \dfrac{3}{2} \Rightarrow y = - 2.{\left( { - \dfrac{3}{2}} \right)^2} = - \dfrac{9}{2}.\)
Vậy hai đồ thị hàm số đã cho cắt nhau tại hai điểm phân biệt: \(\left( {1; - 2} \right)\) và \(\left( { - \dfrac{3}{2}; - \dfrac{9}{2}} \right).\)
Câu 5.
Cách giải:
Cho biểu thức \(P = \left[ {\dfrac{{3x + 3\sqrt x - 3}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 1} \right)}} + \dfrac{1}{{\sqrt x + 2}} - \dfrac{{\sqrt x - 2}}{{\sqrt x - 1}}} \right]:\dfrac{{\sqrt x }}{{\sqrt x + 1}}\) với \(x > 0,\,\,x \ne 1\).
a) Rút gọn biểu thức \(P\).
Với \(x > 0,\,\,x \ne 1\) ta có:
\(\begin{array}{l}P = \left[ {\dfrac{{3x + 3\sqrt x - 3}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 1} \right)}} + \dfrac{1}{{\sqrt x + 2}} - \dfrac{{\sqrt x - 2}}{{\sqrt x - 1}}} \right]:\dfrac{{\sqrt x }}{{\sqrt x + 1}}\\P = \dfrac{{3x + 3\sqrt x - 3 + \left( {\sqrt x - 1} \right) - \left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 1} \right)}}:\dfrac{{\sqrt x }}{{\sqrt x + 1}}\\P = \dfrac{{3x + 3\sqrt x - 3 + \sqrt x - 1 - x + 4}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 1} \right)}}:\dfrac{{\sqrt x }}{{\sqrt x + 1}}\\P = \dfrac{{2x + 4\sqrt x }}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 1} \right)}}.\dfrac{{\sqrt x + 1}}{{\sqrt x }}\\P = \dfrac{{2\sqrt x \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 1} \right)}}.\dfrac{{\sqrt x + 1}}{{\sqrt x }}\\P = \dfrac{{2\left( {\sqrt x + 1} \right)}}{{\sqrt x - 1}}\end{array}\)
Vậy với \(x > 0,\,\,x \ne 1\) thì \(P = \dfrac{{2\left( {\sqrt x + 1} \right)}}{{\sqrt x - 1}}\).
b) Tìm giá trị của \(x\) để \(P > 0\).
Ta có: \(P > 0 \Leftrightarrow \dfrac{{2\left( {\sqrt x + 1} \right)}}{{\sqrt x - 1}} > 0\).
Do \(\sqrt x + 1 > 0\,\,\forall x\) nên \(2\left( {\sqrt x + 1} \right) > 0\,\,\forall x\).
Do đó \(\dfrac{{2\left( {\sqrt x + 1} \right)}}{{\sqrt x - 1}} > 0 \Leftrightarrow \sqrt x - 1 > 0 \Leftrightarrow \sqrt x > 1 \Leftrightarrow x > 1\).
Kết hợp điều kiện ta có \(x > 1\).
Vậy để \(P > 0\) thì \(x > 1\).
Câu 6.
Cách giải:
Ông Minh dự định đi bằng xe máy từ địa điểm A đến địa điểm B cách nhau 80 km trong thời gian định trước. Khi đi được 20 km, tại địa điểm C, xe của ông hỏng nên ông phải dừng lại để sửa xe mất 10 phút. Sau khi sửa xe xong, để đảm bảo thời gian như đã đinh, ông Minh tăng vận tốc thêm 5 km/h trên quãng đường đi từ C đến B. Hãy tính vận tốc xe của ông Minh trên quãng đường từ A đến C.
Gọi vận tốc dự định của ông Minh là \(x\,\,\left( {km/h} \right),\,\,\left( {x > 0} \right).\)
Khi đó thời gian dự định ông Minh đi hết quãng đường từ A đến B là: \(\dfrac{{80}}{x}\,\,\left( h \right).\)
Thời gian ông Minh đi hết quãng đường AC là: \(\dfrac{{20}}{x}\,\,\left( h \right).\)
Sau khi sửa xe, ông Minh đã tăng vận tốc thêm \(5\,km/h\) trên quãng đường CB nên vận tốc ông Minh đi trên quãng đường CB là: \(x + 5\,\,\left( {km/h} \right).\)
Thời gian ông Minh đi hết quãng đường BC là: \(\dfrac{{80 - 20}}{{x + 5}} = \dfrac{{60}}{{x + 5}}\,\,\left( h \right).\)
Tuy phải sửa xe mất \(10\) phút \( = \dfrac{{10}}{{60}} = \dfrac{1}{6}\,\,\left( h \right)\) nhưng ông Minh vẫn đến nơi đúng dự định nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\dfrac{{80}}{x} = \dfrac{{20}}{x} + \dfrac{{60}}{{x + 5}} + \dfrac{1}{6}\\ \Leftrightarrow \dfrac{{60}}{x} - \dfrac{{60}}{{x + 5}} = \dfrac{1}{6}\\ \Leftrightarrow 6.60\left( {x + 5} \right) - 6.60x = x\left( {x + 5} \right)\\ \Leftrightarrow 1800 = {x^2} + 5x\\ \Leftrightarrow {x^2} + 5x - 1800 = 0\\ \Leftrightarrow {x^2} + 45x - 40x - 1800 = 0\\ \Leftrightarrow x\left( {x + 45} \right) - 40\left( {x + 45} \right) = 0\\ \Leftrightarrow \left( {x + 45} \right)\left( {x - 40} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 45 = 0\\x - 40 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 45\,\,\,\left( {ktm} \right)\\x = 40\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy vận tốc của ông Minh đi trên quãng đường AC là 40 km/h.
Câu 7.
Cách giải:
Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(AB = 3cm,\,\,BC = 5cm.\) Tính độ dài cạnh \(AC\) và đường cao \(AH.\)
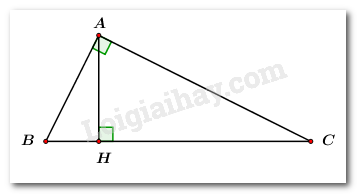
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có:
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{5^2} - {3^2}} = 4\,\,cm.\)
Áp dụng hệ thức lượng cho cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{3.4}}{5} = 2,4\,\,cm.\)
Vậy \(AC = 4\,cm\) và \(AH = 2,4\,cm.\)
Câu 8.
Cách giải:
Cho hai đường tròn \(\left( {{O_1};\,\,10\,cm} \right)\) và \(\left( {{O_2};\,\,15\,cm} \right)\) cắt nhau tại hai điểm phân biệt. Tiếp tuyến chung ngoài \(AB\) cắt đường thẳng \({O_1}{O_2}\) tại điểm \(C\) với \(A \in \left( {{O_1}} \right),\,\,B \in \left( {{O_2}} \right).\) Tính độ dài đoạn thẳng \({O_1}{O_2}\) biết \(C{O_1} = 40\,cm.\)
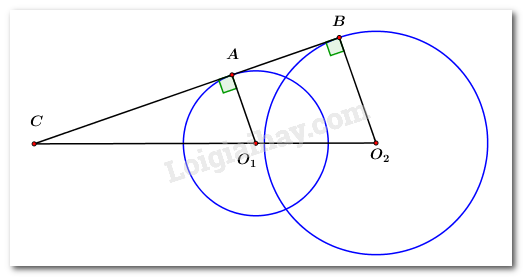
Ta có: \(\left\{ \begin{array}{l}A \in \left( {{O_1}} \right) \Rightarrow {O_1}A = 10\,\,cm\\B \in \left( {{O_2}} \right) \Rightarrow {O_2}B = 15\,cm\end{array} \right..\)
\(AB\) là tiếp tuyến chung ngoài của hai đường tròn \( \Rightarrow \left\{ \begin{array}{l}{O_1}A \bot BC\\{O_2}B \bot BC\end{array} \right..\)
\( \Rightarrow A{O_1}//B{O_2}\) (từ vuông góc đến song song)
\( \Rightarrow \dfrac{{C{O_1}}}{{C{O_2}}} = \dfrac{{A{O_1}}}{{B{O_2}}}\) (định lý Ta-let)
\(\begin{array}{l} \Rightarrow \dfrac{{40}}{{C{O_2}}} = \dfrac{{10}}{{15}} = \dfrac{2}{3}\\ \Rightarrow C{O_2} = \dfrac{{40.3}}{2} = 60\,\,cm.\\ \Rightarrow {O_1}{O_2} = C{O_2} - C{O_1} = 60 - 40 = 20cm.\end{array}\)
Vậy \({O_1}{O_2} = 20\,\,cm.\)
Câu 9.
Cách giải:
Cho tam giác \(ABC\) cân tại \(A,\) các đường cao \(AM,\,\,BN\) cắt nhau tại \(H.\) Chứng minh \(MN\) là tiếp tuyến của đường tròn đường kính \(AH.\)
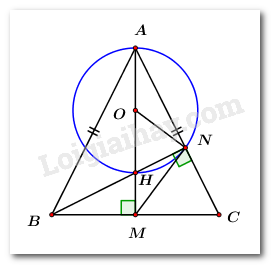
Gọi \(O\) là trung điểm của \(AH\) \( \Rightarrow O\) là tâm của đường tròn đường kính \(AH.\)
Ta có: \(BN\) là đường cao của \(\Delta ABC\) \( \Rightarrow BN \bot AC \Rightarrow \angle HNA = {90^0}\)
\( \Rightarrow \Delta ANH\) vuông tại \(N\) \( \Rightarrow N \in \left( O \right).\) (*)
Xét \(\Delta ANH\) vuông tại \(N\) có đường trung tuyến \(ON\)
\( \Rightarrow ON = OH = \dfrac{1}{2}AH\) (đường trung tuyến ứng với cạnh huyền trong tam giác vuông).
\( \Rightarrow \Delta ONH\) cân tại \(O\) (định nghĩa tam giác cân)
\( \Rightarrow \angle ONH = \angle OHN\) (tính chất tam giác cân) (1)
Vì \(\Delta ABC\) cân tại \(A,\) có đường cao \(AM \Rightarrow M\) là trung điểm của \(BC\) (tính chất \(\Delta \) cân).
Xét \(\Delta BCN\) vuông tại \(N\) có đường trung tuyến \(MN\)
\( \Rightarrow MN = BM = \dfrac{1}{2}BC\) (đường trung tuyến ứng với cạnh huyền trong tam giác vuông).
\( \Rightarrow \angle MBN = \angle MNB\) (tính chất tam giác cân). (2)
Lại có: \(\angle MHB + \angle HBM = {90^0}\) (\(\Delta BHM\)vuông tại \(M\))
Hay \(\angle MHB + \angle NBM = {90^0}\)
Mặt khác \(\angle BHM = \angle OHN\) (hai góc đối đỉnh)
\( \Rightarrow \angle OHN + \angle HBM = {90^0}\) (3)
Từ (1), (2) và (3) ta suy ra: \(\angle MNB + \angle HNO = {90^0}\)
Hay \(MN \bot ON\) (**)
Từ (*) và (**) \( \Rightarrow MN\) là tiếp tuyến của đường tròn đường kính \(AH.\) (đpcm)
Câu 10.
Cách giải:
Cho \(\Delta ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right),\) các đường cao \(AD,\,\,BE,\,\,CF\) cắt nhau tại \(H.\) Đường thẳng \(AD\) cắt đường tròn \(\left( O \right)\) tại \(M \ne A.\)
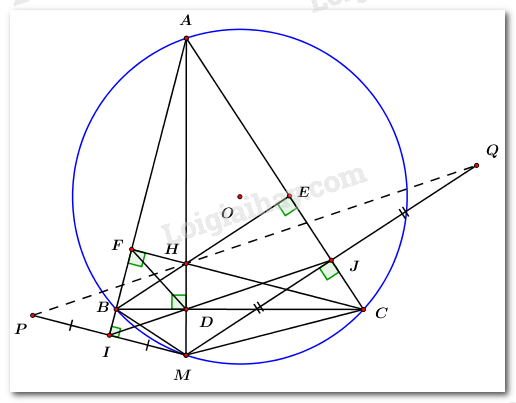
a) Chứng minh \(\Delta BHM\) cân.
Ta có: \(AD,\,\,CF\) là hai đường cao của \(\Delta ABC\) \( \Rightarrow \left\{ \begin{array}{l}CF \bot AB\\AD \bot BC\end{array} \right. \Rightarrow \angle AFC = \angle ADC = {90^0}\)
Xét tứ giác \(ACDF\) ta có:
\(\angle AFC = \angle EDC = {90^0}\)
Mà đỉnh \(F,\,\,D\) là hai đỉnh kề nhau
\( \Rightarrow ACDF\) là tứ giác nội tiếp. (dhnb)
\( \Rightarrow \angle DAC = \angle DFC\) (hai góc nội tiếp cùng chắn cung \(DC\))
Hay \(\angle MAC = \angle DFC.\) (1)
Xét đường tròn \(\left( O \right)\) ta có:
\(\angle MBC\) và \(MAC\) là hai góc nội tiếp cùng chắn cung \(MC\)
\( \Rightarrow \angle MBC = \angle MAC\) (2)
Xét tứ giác \(BFHD\) ta có:
\(\angle BFH + \angle BDH = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện
\( \Rightarrow BFHD\) là tứ giác nội tiếp. (dhnb)
\( \Rightarrow \angle HFD = \angle HBD\) (hai góc nội tiếp cùng chắn cung \(HD\))
Hay \(\angle CFD = \angle HBD\) (3)
Từ (1), (2) và (3) suy ra \(\angle HBD = \angle CBM\) hay \(\angle HBD = \angle DBM\)
\( \Rightarrow BD\) là đường phân giác của \(\Delta BHM\)
Xét \(\Delta HBM\) ta có: \(BD\) vừa là đường cao, vừa là đường phân giác
\( \Rightarrow \Delta BHM\) cân tại \(B.\) (đpcm)
b) Gọi \(P,\,\,Q\) lần lượt là điểm đối xứng với \(M\) qua \(AB\) và \(AC.\) Chứng minh ba điểm \(P,\,\,H,\,\,Q\) thẳng hàng.
Gọi \(I\) là giao điểm của \(AB\) và \(PM,\) \(J\) là giao điểm của \(AC\) mà \(MQ.\)
\( \Rightarrow \left\{ \begin{array}{l}AB \bot PM = \left\{ I \right\}\\AC \bot MQ = \left\{ J \right\}\end{array} \right.\)
Xét tứ giác \(IBDM\) ta có:
\(\angle BIM + \angle BDM = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện
\( \Rightarrow IBDM\) là tứ giác nội tiếp. (dhnb)
\( \Rightarrow \angle IMB = \angle IDB\) (hai góc nội tiếp cùng chắn cung \(IB\)).
Xét tứ giác \(MDJC\) ta có:
\(\angle MDC = \angle MJC = {90^0}\)
Mà hai góc này là hai góc kề nhau
\( \Rightarrow MDJC\) là tứ giác nội tiếp. (dhnb)
\( \Rightarrow \angle JDC = \angle JMC\) (hai góc nội tiếp cùng chắn cung \(JC\))
Tứ giác \(ABMC\) là tứ giác nội tiếp đường tròn \(\left( O \right)\)
\( \Rightarrow \angle IBM = \angle ACM\) (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện). (1)
Ta có: \(\Delta BIM\) vuông tại \(I\) \( \Rightarrow \angle IBM + \angle IMB = {90^0}\) (2)
\(\Delta JMC\) vuông tại \(J\) \( \Rightarrow \angle JMC + \angle JCM = {90^0}\) (3)
Từ (1), (2) và (3) suy ra: \(\angle BMI = \angle BDI = \angle JDC = \angle JMC\)
\( \Rightarrow \angle BDI,\,\,\angle JDC\) là hai góc đối đỉnh
\( \Rightarrow I,\,\,D,\,\,J\) thẳng hàng.
Ta có:\(\Delta BHD\) là tam giác cân tại \(B\) (cmt) có đường cao \(BD\)
\( \Rightarrow D\) là trung điểm của \(HM.\) (tính chất tam giác cân)
Xét \(\Delta PHM\) ta có:
\(D,\,\,I\) lần lượt là trung điểm của \(MH,\,\,MP\)
\( \Rightarrow DI\) là đường trung bình của \(\Delta PHM\)
\( \Rightarrow DI//PH\) (tính chất đường trung bình).
\( \Rightarrow PH//IJ\) (4)
Xét \(\Delta MHQ\) ta có:
\(D,\,\,J\) lần lượt là trung điểm của \(MH,\,\,MQ\)
\( \Rightarrow DJ\) là đường trung bình của \(\Delta MHQ\)
\( \Rightarrow DJ//HQ\) (tính chất đường trung bình).
\( \Rightarrow HQ//IJ\) (5)
Từ (4) và (5) suy ra: \(P,\,\,H,\,\,Q\) thẳng hàng.