Đề bài
Câu 1: Giải các phương trình và hệ phương trình:
\(\begin{array}{l}a)\,\,\,\,\sqrt 2 {x^2} - \sqrt 8 = 0.\\b)\,\,\,2{x^2} + 3x - 2 = 0.\end{array}\)
\(c)\,\,\,\left\{ \begin{array}{l} - x + y = - 5\\3x + 5y = - 1\end{array} \right..\)
Câu 2: Cho hàm số: \(\left( P \right):\,\,y = \dfrac{{ - {x^2}}}{2},\)\(\,\,\,\left( d \right):\,\,y = \dfrac{3}{2}x - 2\)
a) Vẽ đồ thị (P) và (d) trên cùng trục tọa độ Oxy.
b) Tìm tọa độ giao điểm d và P bằng phép toán.
Câu 3: Cho phương trình: \({x^2} + (2m - 3)x - m + 1 = 0\)
a) Chứng minh rằng phương trình luôn có 2 nghiệm \({x_1},\,\,{x_2}\) phân biệt với mọi giá trị của \(m.\)
b) Tìm m để phương trình có 2 nghiệm phân biệt thỏa mãn hệ thức: \(({x_1} - 3)({x_2} - 3) = 5.\)
Câu 4: Cần pha bao nhiêu lít nước ở \({40^0}C\) và 8 lít nước ở \({70^0}C\) để thu được lượng nước \({60^0}C\) ?
Câu 5: Bạn Nam đi học từ nhà đến trường bằng xe đạp có bán kính bánh xe 700mm. Tính quãng đường từ nhà tới trường, biết bánh xe quay tất cả 875 vòng (giả sử bạn Nam đạp xe chạy thẳng từ nhà đến trường trên một đường thẳng và kết quả làm tròn đến chữ số thập phân thứ nhất).
Câu 6: Từ điểm S nằm ngoài (O; R), vẽ hai tiếp tuyến SA, SB (O) (B, C là hai tiếp điểm) và cát tuyến SCD (C nằm giữa S và D, tia SD nằm trong góc ASO).
a) Chứng minh: SAOB là tứ giác nội tiếp và: \(S{A^2} = SD.SC.\)
b) Gọi H là giao điểm AB và OS. Chứng minh rằng: \(\angle DCO = \angle SHC.\)
c) Gọi I là trung điểm của CD. Chứng minh: \(\Delta IAC \backsim \Delta ICB.\)
LG câu 1
Phương pháp giải:
+) Đây là các phương trình bậc 2, ta đưa về phương trình tích để giải.
+) Đối với hệ phương trình bậc nhất 2 ẩn, ta sử dụng phép thế hoặc nhân hệ số rồi trừ 2 vế.
Lời giải chi tiết:
\(\begin{array}{l}a)\,\,\sqrt 2 {x^2} - \sqrt 8 = 0\\ \Leftrightarrow {x^2} = \sqrt 4 = 2\\ \Leftrightarrow x = \pm \sqrt 2 .\end{array}\)
Vậy phương trình có tập nghiệm là: \(S = \left\{ { - \sqrt 2 ;\,\,\sqrt 2 } \right\}.\)
\(\begin{array}{l}b)\,\,2{x^2} + 3x - 2 = 0\\ \Leftrightarrow (2x - 1)(x + 2) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x - 1 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\\x = - 2\end{array} \right..\end{array}\)
Vậy phương trình có tập nghiệm là: \(S = \left\{ { - 2;\,\,\dfrac{1}{2}} \right\}.\)
\(\begin{array}{l}c)\,\,\left\{ \begin{array}{l} - x + y = - 5\\3x + 5y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3x + 3y = - 15\\3x + 5y = - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - x + y = - 5\\8y = - 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - 2\end{array} \right..\end{array}\)
Vậy hệ phương trình có nghiệm là: \(\left( {x;\,y} \right) = \left( {3; - 2} \right).\)
LG câu 2
Phương pháp giải:
1) Lập bảng giá trị các điểm thuộc đồ thị hàm số (P) và vẽ đồ thị hàm số.
2) Lập phương trình hoành độ giao điểm của (d) cắt (P).
+) Để (d) cắt (P) tại hai điểm phân biệt thì phương trình hoành độ giao điểm phải có hai nghiệm phân biệt tức là \(\Delta > 0.\)
Lời giải chi tiết:
Cho hàm số: \(y = \dfrac{{ - {x^2}}}{2}\,\,\,(P),\,\,\,y = \dfrac{3}{2}x - 2\,\,\,(d).\)
a) Vẽ đồ thị (P) và (d) trên cùng trục tọa độ Oxy.
Ta có bảng giá trị:
| \(x\) | \( - 4\) | \( - 2\) | 0 | 2 | 4 |
| \(\;y = - \dfrac{{{x^2}}}{2}\) | \( - 8\) | \( - 2\) | 0 | \( - 2\) | \( - 8\) |
Vậy đồ thị hàm số \(\left( P \right):\,\,y = - \dfrac{{{x^2}}}{2}\) là đường cong đi qua các điểm \(\left( { - 4;\, - 8} \right),\,\,\left( { - 2; - 2} \right),\,\left( {0;\,0} \right),\,\,\left( {2; - 2} \right),\,\,\left( {4; - 8} \right).\)
| \(x\) | 0 | \(2\) |
| \(y = \dfrac{3}{2}x - 2\) | \( - 2\) | \(1\) |
Vậy đồ thị hàm số \(\left( d \right):\,\,y = \dfrac{3}{2}x - 2\) là đường thẳng đi qua các điểm \(\left( {0; - 2} \right),\,\,\left( {2;\,1} \right).\)
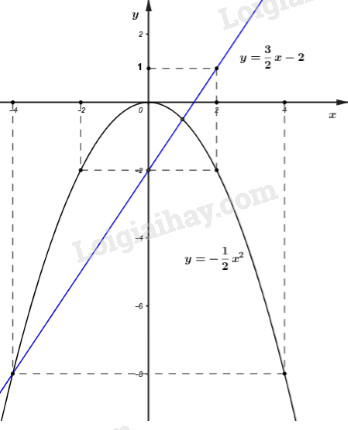
b) Tìm tọa độ giao điểm d và P.
Phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là:
\(\begin{array}{l} - \dfrac{{{x^2}}}{2} = \dfrac{3}{2}x - 2\\ \Leftrightarrow {x^2} + 3x - 4 = 0\\ \Leftrightarrow (x + 4)(x - 1) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 4 = 0\\x - 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 4 \Rightarrow y = - 8\\x = 1 \Rightarrow y = - \dfrac{1}{2}\end{array} \right..\end{array}\)
Vậy tọa độ giao điểm (d) và (P) là: \(\left( { - 4; - 8} \right);\,\,\left( {1; - \dfrac{1}{2}} \right).\)
LG câu 3
Phương pháp giải:
Bước 1: Tìm m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) : Phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) khi và chỉ khi \(\Delta \left( {\Delta '} \right) > 0\)
Bước 2: Phân tích biểu thức A về dạng chứa các hệ thức Viet sau đó áp dụng Viet vào tìm được m và đối chiếu với điều kiện sau đó kết luận. Hệ thức Viet như sau: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)
Lời giải chi tiết:
Cho phương trình: \({x^2} + (2m - 3)x - m + 1 = 0\)
a) Chứng minh rằng phương trình luôn có 2 nghiệm phân biệt.
Ta có:
\(\begin{array}{l}\Delta = {(2m - 3)^2} + 4(m - 1)\\ = 4{m^2} - 12m + 9 + 4m - 4\\ = 4{m^2} - 8m + 5\end{array}\)
\( = {\left( {2m - 2} \right)^2} + 1 > 0\,\) với mọi \(m.\)
Do đó phương trình trên luôn có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) với mọi \(m.\)
b) Tìm m để phương trình có 2 nghiệm phân biệt: \(({x_1} - 3)({x_2} - 3) = 5.\)
Áp dụng định lý Viet ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 3 - 2m\\{x_1}{x_2} = 1 - m\end{array} \right..\)
Theo đề bài ta có : \(\left( {{x_1} - 3} \right)\left( {{x_2} - 3} \right) = 5\)
\(\begin{array}{l} \Leftrightarrow {x_1}{x_2} - 3\left( {{x_1} + {x_2}} \right) + 9 = 5\\ \Leftrightarrow 1 - m - 3\left( {3 - 2m} \right) = - 4\\ \Leftrightarrow 5m = 4 \Leftrightarrow m = \dfrac{4}{5}.\end{array}\)
Vậy giá trị cần tìm của m là : \(m = \dfrac{4}{5}.\)
LG câu 4
Phương pháp giải:
Sử dụng công thức phương trình cân bằng nhiệt: \(Q = mc(t' - t).\)
Lời giải chi tiết:
Gọi lượng nước cần pha thêm là \(x\,\left( {lit} \right),\,\,\,\left( {x > 0} \right).\)
Ta có: 3 lít = 3 kg.
Theo đề bài ta có :
\({Q_1} = {m_1}c({t_1} - t)\)\( = x.4200.(60 - 40)\)
\({Q_2} = {m_2}c({t_2} - t)\)\( = 8.4200.(70 - 60)\)
\(\begin{array}{l} \Rightarrow {Q_1} = {Q_2}\\ \Leftrightarrow x.4200.20 = 8.4200.10\\ \Leftrightarrow x = 4\,\,\left( {tm} \right)\end{array}\)
Vậy cần pha thêm tổng cộng 4 lít nước.
LG câu 5
Phương pháp giải:
Giải bài toán bằng cách lập phương trình:
+) Gọi ẩn và đặt điều kiện cho ẩn.
+) Biểu diễn các đại lượng chưa biết theo ẩn vừa gọi và các đại lượng đã biết.
+) Dựa vào dữ kiện bài toán để lập phương trình.
+) Giải phương trình vừa lập sau đó đối chiếu với điều kiện đề bài và kết luận.
Lời giải chi tiết:
Gọi quãng đường từ nhà bạn Nam đến trường là \(x\,\,\left( {mm} \right),\,\,\left( {x > 0} \right).\)
1 vòng bánh xe quay được 1 chu vi bánh xe là:
\(2\pi r = 2\pi .700 = 1400\pi \,\,\,\left( {mm} \right)\)
\( \Rightarrow x = 1400\pi .875\)\( \approx 3844851\,\,\left( {mm} \right) = 3,844851\,\,\,\left( {km} \right).\)
Vậy chiều dài từ nhà đến trường là: 3,8 km.
LG câu 6
Phương pháp giải:
a) Chứng minh đây là tứ giác có 2 góc đối vuông, từ đó sử dụng tam giác đồng dạng suy ra hệ thức.
b) Chứng minh OICH là tứ giác nội tiếp, tam giác OCD cân.
c) Gọi P là giao điểm SI và AP, chứng minh rằng \(\angle ICA = \angle CBI.\)
Lời giải chi tiết:
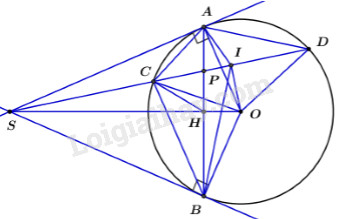
a) Chứng minh: SAOB là tứ giác nội tiếp và: \(S{A^2} = SD.SC.\)
Ta có \(SA,\,\,SB\) là hai tiếp tuyến của \(\left( {O;R} \right)\) tại \(A,\,B\)
\(\begin{array}{l} \Rightarrow \angle SAO = \angle SBO = {90^0}\\ \Rightarrow \angle SAO + \angle SBO = {90^0} + {90^0} = {180^0}\end{array}\)
\( \Rightarrow SAOB\) là tứ giác nội tiếp (dhnb).
Ta có: \(\angle SAC = \angle ADS\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC)
Xét \(\Delta SAC\) và \(\Delta SDA\) ta có:
\(\begin{array}{l}\angle S\,\,\,chung\\\angle SAC = \angle SDA\,\,\left( {cmt} \right)\\ \Rightarrow \Delta SAC \backsim \Delta SDA\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{SA}}{{SD}} = \dfrac{{SC}}{{SA}}\\ \Leftrightarrow S{A^2} = SD.SC\,\,\end{array}\)
b) Gọi H là giao điểm AB và OS. Chứng minh rằng: \(\angle DCO = \angle SHC.\)
Ta có: \(OC = OD = R\)\( \Rightarrow \Delta OCD\) cân tại \(O \Rightarrow \angle CDO = \angle DCO\) (hai góc kề đáy).
Có \(SA = SB\) (tính chất 2 tiếp tuyến cắt nhau) và \(OA = OB = R \Rightarrow SO\) là đường trung trực của \(AB \Rightarrow SO \bot AB = \left\{ H \right\}.\)
Áp dụng hệ thức lượng trong \(\Delta SAO\) có đường cao \(AH\) là có: \(S{A^2} = SH.SO\)
\( \Rightarrow SD.SC = SH.SO\,\,\left( { = S{A^2}} \right)\) \( \Rightarrow \dfrac{{SD}}{{SH}} = \dfrac{{SO}}{{SC}}\)
Xét \(\Delta SOD\) và \(\Delta SCH\) ta có:
\(\begin{array}{l}\dfrac{{SD}}{{SH}} = \dfrac{{SO}}{{SC}}\,\,\,\left( {cmt} \right)\\\angle S\,\,chung\\ \Rightarrow \Delta SOD \backsim \Delta SCH\,\,\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow \angle SHC = \angle DCO\) (hai góc tương ứng).
c) Gọi I là trung điểm của CD. Chứng minh:
Gọi \(SI \cap AB = \left\{ P \right\}.\)
Ta có \(I\) là trung điểm của \(CD \Rightarrow OI \bot CD\) (liên hệ giữa đường kính và dây cung)
\( \Rightarrow \angle OIC = \angle OHA\,\,\,\left( { = {{90}^0}} \right)\) \( \Rightarrow \angle OIC + \angle OHA\, = {180^0}\)
\( \Rightarrow OHPI\) là tứ giác nội tiếp (dhnb).
Xét \(\Delta SPH\) và \(\Delta SOI\) ta có:
\(\begin{array}{l}\angle S\,\,chung\\\angle SHP = \angle SIO = {90^0}\\ \Rightarrow \Delta SPH \backsim \Delta SOI\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{SP}}{{SO}} = \dfrac{{SH}}{{SI}}\\ \Leftrightarrow SP.SI = SH.SO = S{A^2}\\ \Rightarrow \dfrac{{SP}}{{SA}} = \dfrac{{SA}}{{SO}}\end{array}\)
Xét \(\Delta SAP\) và \(\Delta SIA\) ta có:
\(\begin{array}{l}\angle S\,\,chung\\\dfrac{{SP}}{{SA}} = \dfrac{{SA}}{{SO}}\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta SPH \backsim \Delta SOI\,\,\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow \angle SAB = \angle AIC = \angle CIB\) (các góc tương ứng).
Ta có:
\(\angle CAI = \angle SAI - \angle SAC\)
\(= \angle SPA - \angle SAC\)
\(=\dfrac {1}2\) sđ cung BD \( = \angle DCB.\)
Xét \(\Delta IAC\) và \(\Delta ICB\) ta có:
\(\begin{array}{l}\angle AIC = \angle CIB\,\,\left( {cmt} \right)\\\angle ICB = \angle CAI\,\,\left( {cmt} \right)\,\end{array}\)
\( \Rightarrow \Delta IAC \backsim \Delta ICB\,\,\left( {g - g} \right)\) (đpcm)
Nguồn sưu tầm
DapAnHay